题目内容
（请给出正确答案）
[主观题]
设A=（aij)是任意n阶实矩阵。证明（阿达马（Hadamard)不等式)。
设A=(aij)是任意n阶实矩阵。证明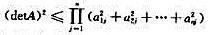
(阿达马(Hadamard)不等式)。
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
设A=(aij)是任意n阶实矩阵。证明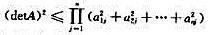(阿达马(Hadamard)不等式)。
如果结果不匹配，请 联系老师 获取答案
更多“设A=（aij)是任意n阶实矩阵。证明（阿达马（Hadama…”相关的问题
证明|A|=1.
设n阶方阵A=(aij)的各行元之和为常数a,证明
(1)a为A的一个特征值,
是对应的特征向量;
(2)Am的每行无之和为am,其中m为正整教;
(3)若A可逆,则A-1的每行元之和为1/a.
设n阶方阵A与B相似,证明:
(1)对任意的正整数k,都有Ak与Bk相似;
(2)对任意一个多项式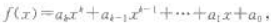
矩阵多项式f(A)和f(B)相似;
(3)当A,B都是可逆矩阵时,An和Bn相似。
已知A=(aij)mxn，B=(bij)mxn，且A，B均可逆，又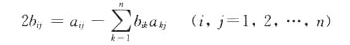
。证明B=E-2(2E+A)-1(其中E为n阶单位矩阵).。
设λ0是n阶方阵A的一个特征值.记A的属于λ0的特征向量的全体及零向量为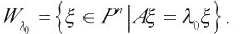
证明: (1) 若ξ1,ξ2∈Wλ0，则ξ1+ξ2∈Wλ0;
(2)若ξ1∈Wλ0，则对任意的k∈P有kξ1∈Wλ0;
(3)由(1)，(2)导出Wλ0为Pn的一个子空间，称为属于λ0的特征子空间，特征子空间Wλ0中任意非零向量都是A的属于λ0的特征向量.
，k=0，1，2，...；aij=si+j-2，i，j=1，2，...，n。证明：
